本文共 3944 字，大约阅读时间需要 13 分钟。

接前一博客。

1、affine坐标系与extended坐标系之间的映射关系

Twisted Edwards curves的affine坐标系表示为：
ε a , d : = { ( x , y ) ∈ P 2 ( F ) : a ∗ x 2 + y 2 = 1 + d ∗ x 2 ∗ y 2 } \varepsilon_{a,d}:=\{(x,y)\in P^2(F):a*x^2+y^2=1+d*x^2*y^2\} εa,d​:={ (x,y)∈P2(F):a∗x2+y2=1+d∗x2∗y2}

对应的Extended坐标系表示为：
ε a , d : = { ( X : Y : Z : T ) ∈ P 3 ( F ) : X Y = Z T   a n d   a ∗ X 2 + Y 2 = Z 2 + d ∗ T 2 } \varepsilon_{a,d}:=\{(X:Y:Z:T)\in P^3(F):XY=ZT\ and\ a*X^2+Y^2=Z^2+d*T^2\} εa,d​:={ (X:Y:Z:T)∈P3(F):XY=ZT and a∗X2+Y2=Z2+d∗T2}
Edwards curve的identity point表示为$(0,1)=(0:1:1:0)$。

affine坐标系与extended坐标系之间的映射关系为：

$$x=X/Z,y=Y/Z,XY=ZT,xy=T/Z$$

2、extended坐标系下的压缩

$s=\sqrt{-a_2\frac{1-y}{1+y}}=\sqrt{-a_2\frac{1-Y/Z}{1+Y/Z}}=\sqrt{-a_2}\frac{Z-Y}{\sqrt{Z^2-Y^2}}$

由此可知，需要计算$1/\sqrt{Z^2-Y^2}$。

根据前一博客第1.3节描述，对于带压缩点$P(x_0,y_0)$需与2-torsion point $(0,-1)或(0,1)$求和，然后根据$xy?>0$，来决定是否需要再需要与点$Q_4$【当$a=1$时，$Q_4=(1,0)$；当$a=-1$时，$Q_4=(i,0),i^2=-1$。因$a^2=1$，可统一描述为$Q_4=(1/\sqrt{a},0)$】求和。


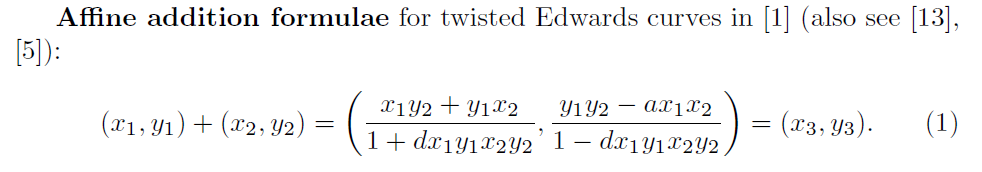
$P(x_0,y_0)\mapsto (x,y)$ affine坐标系下的压缩算法的第一二步内容可梳理为:

• $(x_0,y_0)+(0,1)=(x_0,y_0)$
• 当$x_0{y}_0<=0$时，有$(x_0,y_0)+(1/\sqrt{a},0)=(y_0/\sqrt{a},-\sqrt{a}{x}_0)$

$P(X_0:Y_0:Z_0:T_0)\mapsto (X:Y:Z:T)$衍生到extended坐标系下压缩算法的第一二步内容可梳理为:
$(X:Y:Z:T)=\{\begin{array}{c}(X_0:Y_0:Z_0:T_0)\\ (Y_0/\sqrt{a}:-\sqrt{a}{X}_0:Z_0:-T_0)\end{array}$

$\Rightarrow 1/\sqrt{Z^2-Y^2}=\{\begin{array}{c}1/\sqrt{Z_0^2-Y_0^2}\\ 1/\sqrt{Z_0^2-a{X}_0^2}\end{array}$

同时：
ε a , d : = { ( X : Y : Z : T ) ∈ P 3 ( F ) : X Y = Z T   a n d   a ∗ X 2 + Y 2 = Z 2 + d ∗ T 2 } \varepsilon_{a,d}:=\{(X:Y:Z:T)\in P^3(F):XY=ZT\ and\ a*X^2+Y^2=Z^2+d*T^2\} εa,d​:={ (X:Y:Z:T)∈P3(F):XY=ZT and a∗X2+Y2=Z2+d∗T2}
$\Rightarrow -d{X}^2{Y}^2=Z^4-a{X}^2{Z}^2-Y^2{Z}^2$
$\Rightarrow (a-d)X^2{Y}^2=Z^4-a{X}^2{Z}^2-Y^2{Z}^2+a{X}^2{Y}^2=(Z^2-Y^2)(Z^2-a{X}^2)$
$\Rightarrow \frac{1}{Z^2-a{X}^2}=\frac{1}{a-d}\frac{Z^2-Y^2}{X^2{Y}^2}$
$\Rightarrow \frac{1}{\sqrt{Z^2-a{X}^2}}=\frac{1}{\sqrt{a-d}}\sqrt{\frac{Z^2-Y^2}{X^2{Y}^2}}$

所以，extended坐标系下总的压缩公式计算如下：【其中下图第9步是因为 P + ε a , d [ 2 ] = { ( x , y ) , ( − x , − y ) } P+\varepsilon_{a,d}[2]=\{(x,y),(-x,-y)\} P+εa,d​[2]={ (x,y),(−x,−y)}，即经过上图第一和第二步，所有的点都扭转到了$\frac{\epsilon }{\epsilon [2]}$。】

3、extended坐标系下的解压缩

affine坐标系下，解压缩算法为根据$s$值，求相应的$(x,y)$。
extended坐标系下，解压缩算法为根据$s$值，求相应的$(x,y,1,t)$。

根据前一博客第3节描述有：
$\Rightarrow y=\frac{1+a_2{s}^2}{1-a_2{s}^2}$
$\Rightarrow x=+\sqrt{\frac{4s^2}{a_2{d}_2(1+a_2{s}^2{)}^2-(1-a_2{s}^2{)}^2}}$
extended坐标系下，额外有：
$\Rightarrow t=xy$

所以，总的解压缩公式为：

参考资料：
[1] https://ristretto.group/details/encoding_in_extended.html

转载地址：http://ebqx.baihongyu.com/